Game theory & social media (3): What are you playing at?

[Part 3 of 4: Game theory & social media: Part 1, Part 2, Part 4]

Whatever else anything is, it ought to begin with being personal

Kathleen Kelly, You’ve got mail (1998)

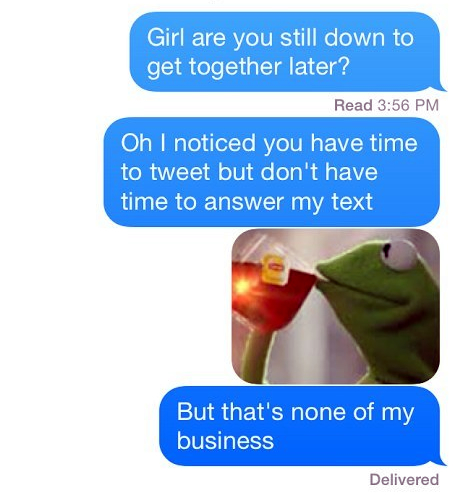
Kermit drinking his tea and throwing shade makes me laugh. However, I think we all understand his frustration. It seems that in business and personal relationships, people play games. We may not know why, and we may not know the rules. But as we saw in part 2, before we react, we might want to find out more: if a game is being played, which one, and if we want to play or not.

Games, payoffs, and winning

A game is normally defined as having two or more players, who have a choice of possible strategies to play which determine the outcome of a game. Each outcome has a payoff which is calculated numerically to represent its value. Usually, a player will want to get the biggest payoff possible in order to be certain of winning.

Dominance, saddles, and mixed strategies

Playing the strategy with the biggest payoff is known as the Dominance Strategy, and a rational player would never do otherwise, but it’s not always easy to identify which strategy is best.

So, players sometimes take a cautious approach which will guarantee a favourable result (also known as the Saddle Point Principle). Other times, there is no saddle point so players have to choose at random what strategy to play and hope for the best. They can calculate the probability of mixing up strategies and their chances of winning. If their probability skills are not great they can play experimentally and record their results 30 times (for statistical significance) to see which strategies work.

How does this work on social media? Well, no one knows how social media works so a trial and error approach whilst recording results can be useful. Luckily, Twitter and Facebook both provide services and stats to help.

Free will, utility, and Pareto’s principle

A major question is whether players have free will or not and whether their choices are predetermined based on who they are playing with and the circumstances in which the game takes place. This can depend on the amount of information players have available to them,  and as new information becomes available, they play a specific strategy, thus seeming as if they didn’t have free will at all.

Players assign numbers to describe the value of the outcomes (known in economics as utility theory) which they can use to guide themselves to the most valued outcome.

This is useful if we have a game where the winner doesn’t necessarily take all. If the players have interests which are not opposed and by cooperating the players can end up potentially with a win-win situation or at least a situation where everyone gains some benefits and the solution is not the worst outcome for everyone involved. This is known as the Pareto Principle.

On social media? Retweeting and sharing other’s businesses news is a nice way of ensuring everyone gains some benefits because with a potential market of 307 millions and there is enough of a market to go around for everyone to win-win and of course, reciprocate.

The Nash equilibrium

Taking this further is the Nash equilibrium which was named after John Nash, who proved that every two player game has one equalizing strategy (either pure or mixed) in each game. By looking at the equilibrium strategies of the other players, everyone plays to equalize. This is because, no player has anything to gain by changing only his or her own strategy, so it is win-win.

Are you chicken?

Ducks have been known share out the bread thrown to them so they all get some rather than one duck eating everything. This is known as the Hawk-Dove approach in game theory. When there is competition for a shared resource, players can choose either conciliation or conflict.

Research has shown that when a player is naturally a hawk (winner takes all) and plays amongst doves, then the player will adapt and cooperate. Conversely a dove amongst hawks will adapt too and turn into a fighter.

If there are two hawks playing each other the game is likely to go chicken, which is when both players will risk everything (known as mutually assured destruction in warfare) not to yield first.

We adapt very easily to what is going on around us, and on social media this is totally the same. In a 2014 study Pew Research Center found that people are less likely to share their honest opinions on social media, and will often only post opinions on Facebook with which they know their followers will agree – we like to conform.

The volunteer’s dilemma

In contrast, the volunteer’s dilemma is an altruistic approach where one person does the right thing for the benefit of everyone. For example, one meerkat will look out for predators, at the risk of getting eaten, whilst the rest of the meerkats look for food. And, we admire this too. We love a hero, a maverick, someone who is ready to stand up and be different.

The prisoner’s dilemma

But we hated to feel duped which is why the prisoner’s dilemma is one of the most popular game theories of all. Created by Albert W. Tucker in 1950, it is as follows:

Two prisoners are arrested for a joint crime and put in separate interrogation rooms. The district attorney sets out these rules:

1. If one of them confesses and the other doesn’t, the confessor serves a longer sentence, the other one goes free.
2. If both confess each will get a light sentence.
3. If neither confesses they both serve the longer sentence.

It is in each prisoner’s interest to confess (dominant strategy = 1) and if they both do that satisfies the Pareto principle (2). However, if they both confess, they are better off than if neither do (3).

The prisoner’s dilemma embodies the struggle between individual rationality and group rationality which Nigel Howard described as a metagame of a prisoner cooperating if and only if, they believe that the other prisoner will cooperate, if and only if, they believe that the first prisoner will cooperate. A mind boggling tit-for-tat. But, this is common on Twitter with those: Follow me, I will follow you back and constant following and unfollowing.

And, in any transaction we hate feeling like we have been had, that we were a chump, that we trusted when we shouldn’t have, which is why some people are so angry and like to retaliate. Anger feels better than feeling vulnerable does. But, great daring starts with vulnerability, the fear of failure, and even the failure to start, the hero’s quest shows us that.

Promises, threats, and coalitions

As we add more players, all rationality may go out of the window as players decide whether to form coalitions or to perform strategic style voting. If we introduce the idea of the players communicating then we add the issues of trust in promises, or fear of threats and it all starts to sound rather Hunger Games.

On social media aggression and threats are common, because of prejudice, or group think, especially on Twitter where there is no moderation. And, online and off, we have all been promised things and relationships which have ultimately left us disappointed, and told us that we have been misinformed, like the fake news, we’ve been hearing about a lot lately.  Fake news is not new, in other contexts it is known as propaganda.  And, if it is not completely fake, just exaggerated, well that’s not new either, New Labour loved spin which led to a sexed up dossier, war and death.

Kermit’s next move

Philip D. Straffin says in his book Game theory and strategy, that game theory only works up to a point, after which a player must ask for some clarification about what is going on because mathematics applied to human behaviour will only explain so much.

And so we turn back to Kermit. What is he to do?  He has passive-aggressively asked for clarification and had a cup of tea. What’s his next move? Well, he could wait and see if he gets a reply (tit for tat). Who will crack first (chicken)? But, with the texts he has sent her, it is likely that her response is somewhat predetermined, or perhaps not, perhaps she will repond with Nash’s equilibria, or at the very least the Pareto principle of everyone not getting the worst outcome.

Alternatively, he could take a breath and remember that he is talking to someone he likes and with whom he wants to spend some time, someone human with the same vulnerabilities as him. He could adopt the volunteer’s dilemma approach and send her an honest text to explain that his feelings are hurt, he thought they had something special, and that she liked communicating with him as much as other people. By seeking clarification in this way, Kermit may just end up having a very nice evening after all –  or not. Whoever said: All’s fair in love and war, didn’t have instant access to social media and all the complications it can cause.

[Part 4]